MAGEMin

Problem Definition

Finding the most stable phase assemblage is a challenging constrained optimization problem including both equality and inequality constraints. One has to minimize the Gibbs energy (1) of the system while satisfying the Gibbs-Duhem (2) and mass equality constraints (3) while also satisfying the mixing-in-sites inequality constraints (4).

1. Total Gibbs Energy

The Gibbs energy of a multi-component multiphase system is given by the weighted summation of the chemical potentials of all end-members and pure phases:

\begin{array}{r} G_{s y s} = \sum_{λ = 1}^{Λ} n_{λ} \sum_{i = 1}^{N_{λ}} μ_{i} (λ) p_{i} (λ) + \sum_{ω = 1}^{Ω} n_{ω} μ_{ω} \end{array}

where $n_{λ}$ is the molar fraction of the solution phase, $p_{λ}$ is the molar fraction of the endmembers, and $n_{ω}$ is the molar fraction of the pure phase.

The chemical potential of a phase is either a constant for a condensed (pure) phase:

\begin{array}{r} μ_{i} = G_{i}^{0} \end{array}

or a function for a phase within a solution:

\begin{array}{r} μ_{i} = G_{i}^{0} + R T \log (a_{i}) + G_{i}^{e x} \end{array}

where $a_{i}$ is the thermochemical activity related to the mole fraction and the activity coefficient by:

\begin{array}{r} a_{i} = x_{i} γ_{i} \end{array}

For the case of ideal mixing between the end-members, the activity coefficient is unity. The mixing of a species dissolved in a condensed phase, however, rarely behaves ideally and is typically a function of both temperature and composition (mixing-on-sites formulation).

2. Gibbs-Duhem Constraint

The Gibbs-Duhem constraint is defined as:

\begin{array}{r} \sum_{j = 1}^{C} Γ_{j} a_{i j} - μ_{i} = 0 \end{array}

where $Γ_{j}$ is the chemical potential of pure component (oxide) $j$ and $a_{i j}$ is the molar composition of component $j$ in end-member/pure phase $i$ .

3. Mass Constraint

The mass equality constraint is defined as:

\begin{array}{r} \sum_{λ = 1}^{Λ} n_{λ} \sum_{i = 1}^{N_{λ}} a_{i j} (λ) p_{i} (λ) + \sum_{ω = 1}^{Ω} n_{ω} a_{ω j} - b_{j} = 0 \end{array}

where $a_{i j}$ is the molar composition of component $j$ in end-member $i$ , and $a_{ω j}$ is the molar composition of component $j$ in a pure phase.

Minimization Approach

The Gibbs minimization approach employed in MAGEMin combines discretization of the equations of state in composition space with linear programming and extends the mass-constrained Gibbs-hyperplane rotation method to account for the mixing-on-sites that takes place in silicate mineral solid solutions. For an exhaustive description of the methodology, see Riel et al. (2022).

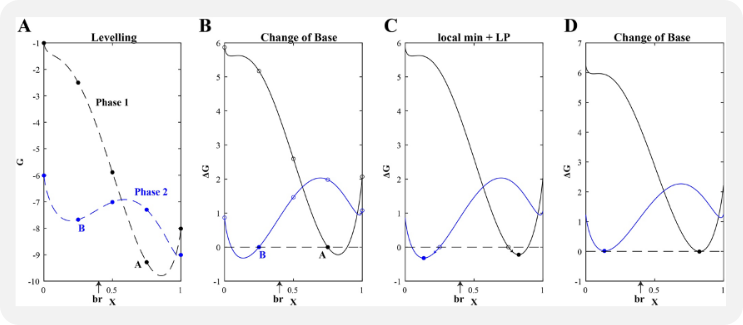
Algorithm Demonstration

A simplified example of the Gibbs energy minimization approach used in MAGEMin is provided at:

GitHub Repository

This MATLAB application includes two pure phases, sillimanite and quartz, and activity-composition (a-x) relations for feldspar (pl4T, Holland et al., 2021) in a reduced Na2O-CaO-K2O-Al2O3-SiO2 (NCKAS) chemical system.

Solvus phase naming

A solvus is a boundary that defines the limit of solid solubility (miscibility) of phases described by the same solution model (or a-x model). It separates a single solid phase from a region where two (or more) distinct solid phases coexist due to compositional differences.

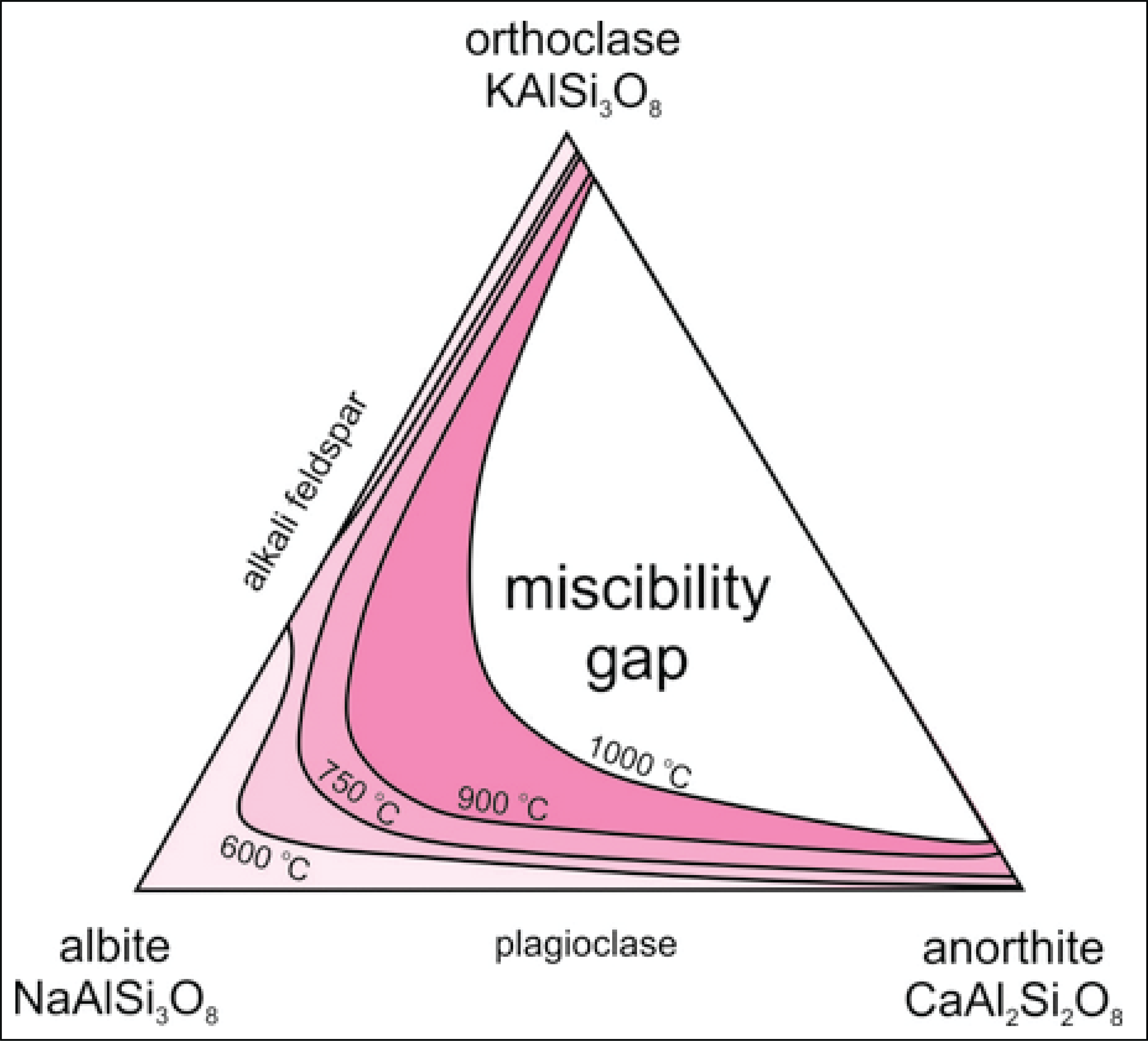
Properly naming demixed phases is important as it allows to differentiate multiple stable instances of the same solution model e.g., plagioclase and alkali-felspar (feldspar) or muscovite and paragonite (muscovite) etc. While for some solution models, naming (or classifying) the demixed phases is relatively straigthforward (e.g., for feldspar) for other solution phases, such as amphibole, the classification rules are more complex and sometimes not fully accurate.

Igneous, igneous alkali dry (ig, igad)

x = SS_vec.compVariables

spinel: spl

julia

if x[3] - 0.5 > 0.0;        mineral_name = "cm"
elseif x[4] - 0.5 > 0.0;    mineral_name = "usp"
elseif x[2] - 0.5 > 0.0;    mineral_name = "mgt"
else                        mineral_name = "spl"

feldspar: fsp

julia

if x[2] - 0.5 > 0.0;        mineral_name = "afs"
else                        mineral_name = "pl";

muscovite: mu

julia

if x[4] - 0.5 > 0.0;        mineral_name = "pat"
else                        mineral_name = "mu"

amphibole: amp

julia

if x[3] - 0.5 > 0.0;        mineral_name = "gl"
elseif -x[3] -x[4] + 0.2 > 0.0;   mineral_name = "act"
else
    if x[6] < 0.1;          mineral_name = "cumm"
    elseif -1/2*x[4]+x[6]-x[7]-x[8]-x[2]+x[3]>0.5;      mineral_name = "tr"    
    else                    mineral_name = "amp"

ilmenite: ilm

julia

if -x[1] + 0.5 > 0.0;       mineral_name = "hem"
else                        mineral_name = "ilm"

nepheline: nph

julia

if x[2] - 0.5 > 0.0;       mineral_name = "K-nph"
else                        mineral_name = "nph"

clinopyroxene: cpx

julia

if x[3] - 0.6 > 0.0;        mineral_name = "pig"
elseif x[4] - 0.5 > 0.0;    mineral_name = "Na-cpx"
else                        mineral_name = "cpx"

metapelite, metabasite, ultramafic (mp, mb, um, mpe, mbe, ume)

x = SS_vec.compVariables

feldspar: fsp

julia

if x[2] - 0.5 > 0.0;        mineral_name = "afs"
else                        mineral_name = "pl";

muscovite: mu

julia

if x[4] - 0.5 > 0.0;        mineral_name = "pat"
else                        mineral_name = "mu"

spinel: sp

julia

if x[2] - 0.5 > 0.0;        mineral_name = "sp"
else                        mineral_name = "mt"

amphibole: amp

julia

if x[3] - 0.5 > 0.0;        mineral_name = "gl"
elseif -x[3] -x[4] + 0.2 > 0.0;   mineral_name = "act"
else
    if x[6] < 0.1;          mineral_name = "cumm"
    elseif -1/2*x[4]+x[6]-x[7]-x[8]-x[2]+x[3]>0.5;      mineral_name = "tr"    
    else                    mineral_name = "amp"

ilmenitem: ilmm

julia

if x[1] - 0.5 > 0.0;        mineral_name = "ilmm"
else                        mineral_name = "hemm"

ilmenite: ilm

julia

if 1.0 - x[1] > 0.5;        mineral_name = "hem"
else                        mineral_name = "ilm"

diopside: dio

julia

if x[2] > 0.0 && x[2] <= 0.3;       mineral_name = "dio"
elseif x[2] > 0.3 && x[2] <= 0.7;   mineral_name = "omph"
else                                mineral_name = "jd"

diopside: occm

julia

if x[2] > 0.5;              mineral_name = "sid"
elseif x[3] > 0.5;          mineral_name = "ank"
elseif x[1] > 0.25 && x[3] < 0.01;         mineral_name = "mag"
else                        mineral_name = "cc"

ortho-amphibole: oamp

julia

if x[2] < 0.3;              mineral_name = "anth"
else                        mineral_name = "ged"

List of mineral abbreviations (for solvus)

Acronym	Full Mineral Name
act	Actinolite
afs	Alkali Feldspar
amp	Amphibole
ank	Ankerite
anth	Anthophyllite
cc	Calcite
cm	Chromite
cpx	Clinopyroxene
cumm	Cummingtonite
dio	Diopside
fsp	Feldspar
ged	Gedrite
gl	Glaucophane
hem/hemm	Hematite
ilm/ilmm	Ilmenite
jd	Jadeite
K-nph	Potassic Nepheline
mt/mgt/mag	Magnetite
mu	Muscovite
nph	Nepheline
Na-cpx	Sodium Clinopyroxene
occm	Carbonate (calcite group)
oamp	Ortho-amphibole
omph	Omphacite
pat	Paragonite
pig	Pigeonite
pl	Plagioclase
sid	Siderite
sp/spl	Spinel
tr	Tremolite
usp	Ulvöspinel

References

Holland, T. J. B., Green, E. C. R., & Powell, R. (2021). A thermodynamic model for feldspars in KAlSi3O8-NaAlSi3O8-CaAl2Si2O8 for mineral equilibrium calculations.
Riel N., Kaus B.J.P., Green E.C.R., Berlie N., (2022) MAGEMin, an Efficient Gibbs Energy Minimizer: Application to Igneous Systems. Geochemistry, Geophysics, Geosystems 23, e2022GC010427 https://doi.org/10.1029/2022GC010427

Problem Definition ​

1. Total Gibbs Energy ​

2. Gibbs-Duhem Constraint ​

3. Mass Constraint ​

Minimization Approach ​

Algorithm Demonstration ​

Solvus phase naming ​

Igneous, igneous alkali dry (ig, igad) ​

metapelite, metabasite, ultramafic (mp, mb, um, mpe, mbe, ume) ​

List of mineral abbreviations (for solvus) ​

References ​

Problem Definition

1. Total Gibbs Energy

2. Gibbs-Duhem Constraint

3. Mass Constraint

Minimization Approach

Algorithm Demonstration

Solvus phase naming

Igneous, igneous alkali dry (ig, igad)

metapelite, metabasite, ultramafic (mp, mb, um, mpe, mbe, ume)

List of mineral abbreviations (for solvus)

References