MAGEMin_C.jl: Examples
This page provides a set of quick examples showing how to use MAGEMin_C.jl to perform phase equilibrium calculations.
Info
Examples 1 to 8 are simple exercises to make you familiar with the various options available for the calculation
Examples 9 to 11 are more advanced and some basic background in Julia programming are recommanded
Note
- The examples are not optimized for performances, but are provided in hope they can be useful to present
MAGEMin_Cfunctionality.
Quickstart examples
E.1 Predefined compositions
This is an example of how to use it for a predefined bulk rock composition:
using MAGEMin_C
db = "ig" # database: ig, igneous (Holland et al., 2018); mp, metapelite (White et al 2014b)
data = Initialize_MAGEMin(db, verbose=true);
test = 0 #KLB1
data = use_predefined_bulk_rock(data, test);
P = 8.0;
T = 800.0;
out = point_wise_minimization(P,T, data);which gives
Status : 0
Mass residual : +5.34576e-06
Rank : 0
Point : 1
Temperature : +800.00000 [C]
Pressure : +8.00000 [kbar]
SOL = [G: -797.749] (25 iterations, 39.62 ms)
GAM = [-979.481432,-1774.104523,-795.261024,-673.747244,-375.070247,-917.557241,-829.990582,-1023.656703,-257.019268,-1308.294427]
Phase : spn cpx opx ol
Mode : 0.02799 0.14166 0.24228 0.58807Note
Thermodynamic dataset acronym are the following:
mtl-> mantle (Holland et al., 2013)mp-> metapelite (White et al., 2014)mb-> metabasite (Green et al., 2016)ig-> igneous (Green et al., 2025 updated from and replacing Holland et al., 2018)igad-> igneous alkaline dry (Weller et al., 2024)um-> ultramafic (Evans & Frost, 2021)sb11-> Stixrude & Lithgow-Bertelloni (2011)sb21-> Stixrude & Lithgow-Bertelloni (2021)ume-> ultramafic extended (Green et al., 2016 + Evans & Frost, 2021)mpe-> extended metapelite (White et al., 2014 + Green et al., 2016 + Franzolin et al., 2011 + Diener et al., 2007)mbe-> extended metabasite (Green et al., 2016 + Diener et al., 2007 + Rebay et al., 2022)
E.2 Minimization output
in the previous example the results of the minimization are saved in a structure called out. To access all the information stored in the structure simply do:
out.Then press tab (tabulation key) to display all stored data:
out.
G_system Gamma MAGEMin_ver M_sys PP_vec P_kbar SS_vec T_C V Vp Vp_S Vs Vs_S X
aAl2O3 aFeO aH2O aMgO aSiO2 aTiO2 alpha bulk bulkMod bulkModulus_M bulkModulus_S bulk_F bulk_F_wt bulk_M
bulk_M_wt bulk_S bulk_S_wt bulk_res_norm bulk_wt cp dQFM dataset enthalpy entropy fO2 frac_F frac_F_wt frac_M
frac_M_wt frac_S frac_S_wt iter mSS_vec n_PP n_SS n_mSS oxides ph ph_frac ph_frac_vol ph_frac_wt ph_id
ph_type rho rho_F rho_M rho_S s_cp shearMod shearModulus_S status time_msIn order to access any of these variables type for instance:
out.fO2which will give you the oxygen fugacity:
out.fO2
-4.405735414252153to access the list of stable phases and their fraction in mol:
out.ph
4-element Vector{String}:
"liq"
"g"
"sp"
"ru"
out.ph_frac
4-element Vector{Float64}:
0.970482189810529
0.003792750364729876
0.020229088594267013
0.0054959712304740085Chemical potential of the pure components (oxides) of the system is retrieved as:
out.Gamma
11-element Vector{Float64}:
-1017.3138187719679
-1847.7215909497188
-881.3605772634041
-720.5475835413267
-428.1896629304572
-1051.6248892195592
-1008.7336303031074
-1070.7332593397723
-228.07833391903714
-561.1937065530427
-440.764181608507
out.oxides
11-element Vector{String}:
"SiO2"
"Al2O3"
"CaO"
"MgO"
"FeO"
"K2O"
"Na2O"
"TiO2"
"O"
"MnO"
"H2O"The composition in wt of the first listed solution phase ("liq") can be accessed as
out.SS_vec[1].Comp_wt
11-element Vector{Float64}:
0.6174962747665693
0.1822124172602761
0.006265730986600257
0.0185105629478801
0.04555393290694774
0.038161590650707795
0.013329583423813463
0.0
0.0
0.0
0.07846990705720527and the end-member fraction in wt and their names as
out.SS_vec[1].emFrac_wt
8-element Vector{Float64}:
0.4608062343057727
0.0972375952287159
0.17818888101139307
0.02313962538195582
0.12734359573100587
0.025819902698522926
0.047571646835750894
0.03989251880688298
out.SS_vec[1].emNames
8-element Vector{String}:
"q4L"
"abL"
"kspL"
"anL"
"slL"
"fo2L"
"fa2L"
"h2oL"E.3 Custom composition
And here a case in which you specify your own bulk rock composition.
using MAGEMin_C
data = Initialize_MAGEMin("ig", verbose=false);
P,T = 10.0, 1100.0
Xoxides = ["SiO2"; "Al2O3"; "CaO"; "MgO"; "FeO"; "Fe2O3"; "K2O"; "Na2O"; "TiO2"; "Cr2O3"; "H2O"];
X = [48.43; 15.19; 11.57; 10.13; 6.65; 1.64; 0.59; 1.87; 0.68; 0.0; 3.0];
sys_in = "wt"
out = single_point_minimization(P, T, data, X=X, Xoxides=Xoxides, sys_in=sys_in)which gives:
Pressure : 10.0 [kbar]
Temperature : 1100.0 [Celsius]
Stable phase | Fraction (mol fraction)
liq 0.75133
cpx 0.20987
opx 0.03877
Stable phase | Fraction (wt fraction)
liq 0.73001
cpx 0.22895
opx 0.04096
Gibbs free energy : -916.874646 (45 iterations; 86.53 ms)
Oxygen fugacity : 2.0509883251350577e-8After the calculation is finished, the structure out holds all the information about the stable assemblage, including seismic velocities, melt content, melt chemistry, densities etc. You can show a full overview of that with
print_info(out)If you are interested in the density or seismic velocity at the point, access it with
out.rho
2755.2995530913095
out.Vp
3.945646731595539Once you are done with all calculations, release the memory with
Finalize_MAGEMin(data)E.4 Export data to CSV
Using previous example to compute a point:
using MAGEMin_C
dtb = "ig"
data = Initialize_MAGEMin(dtb, verbose=false);
P,T = 10.0, 1100.0
Xoxides = ["SiO2"; "Al2O3"; "CaO"; "MgO"; "FeO"; "Fe2O3"; "K2O"; "Na2O"; "TiO2"; "Cr2O3"; "H2O"];
X = [48.43; 15.19; 11.57; 10.13; 6.65; 1.64; 0.59; 1.87; 0.68; 0.0; 3.0];
sys_in = "wt"
out = single_point_minimization(P, T, data, X=X, Xoxides=Xoxides, sys_in=sys_in)Exporting the result of the minimization(s) to an CSV file is straightforward:
MAGEMin_data2dataframe(out,dtb,"filename")where out is the output structure, dtb is the database acronym and "filename" is the filename 😃
The output structure can also be saved as inlined i.e., that every line of the .csv file will output one pressure-temperature phase equilibrium calculation:
MAGEMin_data2dataframe_inlined(out,dtb,"filename")Note
You don't have to add the file extension
.csvThe output path (MAGEMin_C directory) is displayed in the Julia terminal
For multiple points, simply provide the
JuliaVector{out}. See Example 8 for more details on how to create a vector of minimization output.
E.5 Removing solution phase from consideration
To suppress solution phases from the calculation, define a remove list rm_list using the remove_phases() function. In the latter, provide a vector of the solution phase(s) you want to remove and the database acronym as a second argument. Then pass the created rm_list to the single_point_minimization() function.
using MAGEMin_C
data = Initialize_MAGEMin("mp", verbose=-1, solver=0);
rm_list = remove_phases(["liq","sp"],"mp");
P,T = 10.713125, 1177.34375;
Xoxides = ["SiO2","Al2O3","CaO","MgO","FeO","K2O","Na2O","TiO2","O","MnO","H2O"];
X = [70.999,12.805,0.771,3.978,6.342,2.7895,1.481,0.758,0.72933,0.075,30.0];
sys_in = "mol";
out = single_point_minimization(P, T, data, X=X, Xoxides=Xoxides, sys_in=sys_in,rm_list=rm_list)which gives:
Pressure : 10.713125 [kbar]
Temperature : 1177.3438 [Celsius]
Stable phase | Fraction (mol fraction)
fsp 0.29236
g 0.13786
ilmm 0.01526
q 0.22534
sill 0.10705
H2O 0.22213
Stable phase | Fraction (wt fraction)
fsp 0.34544
g 0.17761
ilmm 0.0261
q 0.25385
sill 0.12197
H2O 0.07503
Stable phase | Fraction (vol fraction)
fsp 0.31975
g 0.10873
ilmm 0.01307
q 0.23367
sill 0.08991
H2O 0.23487
Gibbs free energy : -920.021202 (25 iterations; 27.45 ms)
Oxygen fugacity : -5.4221261006295105
Delta QFM : 2.506745293747623Note
Note that if you want to suppress a single phase, you still need to define a vector to be passed to the remove_phases() function, such as shown below.
using MAGEMin_C
data = Initialize_MAGEMin("mp", verbose=-1, solver=0);
rm_list = remove_phases(["liq"],"mp");
P,T = 10.713125, 1177.34375;
Xoxides = ["SiO2","Al2O3","CaO","MgO","FeO","K2O","Na2O","TiO2","O","MnO","H2O"];
X = [70.999,12.805,0.771,3.978,6.342,2.7895,1.481,0.758,0.72933,0.075,30.0];
sys_in = "mol";
out = single_point_minimization(P, T, data, X=X, Xoxides=Xoxides, sys_in=sys_in,rm_list=rm_list)which gives:
Pressure : 10.713125 [kbar]
Temperature : 1177.3438 [Celsius]
Stable phase | Fraction (mol fraction)
fsp 0.29337
g 0.12
sp 0.03036
q 0.23953
sill 0.08939
ru 0.00521
H2O 0.22213
Stable phase | Fraction (wt fraction)
fsp 0.34667
g 0.15368
sp 0.04514
q 0.26983
sill 0.10184
ru 0.00781
H2O 0.07503
Stable phase | Fraction (vol fraction)
fsp 0.31981
g 0.09422
sp 0.02492
q 0.24761
sill 0.07484
ru 0.00446
H2O 0.23413
Gibbs free energy : -920.00146 (19 iterations; 27.79 ms)
Oxygen fugacity : -5.760704474307317
Delta QFM : 2.1681669200698166E.6 Oxygen buffer
Here we need to initialize MAGEMin with the desired buffer (qfm in this case, see list at the beginning).
Note
Note that O/Fe2O3 value needs to be large enough to saturate the system. Excess oxygen-content will be removed from the output
using MAGEMin_C
data = Initialize_MAGEMin("ig", verbose=false, buffer="qfm");
P,T = 10.0, 1100.0
Xoxides = ["SiO2","Al2O3","CaO","MgO","FeO","K2O","Na2O","TiO2","O","Cr2O3","H2O"];
X = [48.43; 15.19; 11.57; 10.13; 6.65; 1.64; 0.59; 1.87; 4.0; 0.1; 3.0];
sys_in = "wt"
out = single_point_minimization(P, T, data, X=X, Xoxides=Xoxides, sys_in=sys_in)Buffer offset in the log10 scale can be applied as
using MAGEMin_C
data = Initialize_MAGEMin("ig", verbose=false, buffer="qfm");
P,T = 10.0, 1100.0
Xoxides = ["SiO2","Al2O3","CaO","MgO","FeO","K2O","Na2O","TiO2","O","Cr2O3","H2O"];
X = [48.43; 15.19; 11.57; 10.13; 6.65; 1.64; 0.59; 1.87; 4.0; 0.1; 3.0];
offset = -1.0
sys_in = "wt"
out = single_point_minimization(P, T, data, X=X, Xoxides=Xoxides, B=offset, sys_in=sys_in)Note
Several buffers can be used to fix the oxygen fugacity
qfm-> quartz-fayalite-magnetiteqif-> quartz-iron-fayalitenno-> nickel-nickel oxidehm-> hematite-magnetiteiw-> iron-wüstitecco-> carbon dioxide-carbon
E.7 Activity buffer
Like for oxygen buffer, activity buffer can be prescribe as follow
Note
Note that the corresponding oxide-content needs to be large enough to saturate the system. Excess oxide-content will be removed from the output
using MAGEMin_C
data = Initialize_MAGEMin("ig", verbose=false, buffer="aTiO2");
P,T = 10.0, 700.0
Xoxides = ["SiO2","Al2O3","CaO","MgO","FeO","K2O","Na2O","TiO2","O","Cr2O3","H2O"];
X = [48.43; 15.19; 11.57; 10.13; 6.65; 1.64; 0.59; 4.0; 0.1; 0.1; 3.0];
value = 0.9
sys_in = "wt"
out = single_point_minimization(P, T, data, X=X, Xoxides=Xoxides, B=value, sys_in=sys_in)Note
Similarly activity can be fixed for the following oxides
aH2O-> using water as reference phaseaO2-> using dioxygen as reference phaseaMgO-> using periclase as reference phaseaFeO-> using ferropericlase as reference phaseaAl2O3-> using corundum as reference phaseaTiO2-> using rutile as reference phaseaSiO2-> using quartz/coesite as reference phase
E.8 Many points
using MAGEMin_C
db = "ig" # database: ig, igneous (Holland et al., 2018); mp, metapelite (White et al 2014b)
data = Initialize_MAGEMin(db, verbose=false);
test = 0 #KLB1
n = 1000
P = rand(8.0:40,n);
T = rand(800.0:2000.0, n);
out = multi_point_minimization(P,T, data, test=test);
Finalize_MAGEMin(data)By default, this will show a progressbar (which you can deactivate with the progressbar=false option).
You can also specify a custom bulk rock for all points (see above), or a custom bulk rock for every point.
Advanced examples
E.9 Fractional crystallization
The following example shows how to perform fractional crystallization using a hydrous basalt magma as a starting composition. The results are displayed using PlotlyJS. This example is provided in the hope it may be useful for learning how to use MAGEMin_C for more advanced applications.
Note
Note that if we wanted to use a buffer, we would need to initialize MAGEMin as in example 4. Because during fractional crystallization the bulk-rock composition is updated at every step, we would need to increase the oxygen-content (O) of the new bulk-rock
using MAGEMin_C
using PlotlyJS
# number of computational steps
nsteps = 64
# Starting/ending Temperature [°C]
T = range(1200.0,600.0,nsteps)
# Starting/ending Pressure [kbar]
P = range(3.0,0.1,nsteps)
# Starting composition [mol fraction], here we used an hydrous basalt; composition taken from Blatter et al., 2013 (01SB-872, Table 1), with added O and water saturated
oxides = ["SiO2"; "Al2O3"; "CaO"; "MgO"; "FeO"; "K2O"; "Na2O"; "TiO2"; "O"; "Cr2O3"; "H2O"]
bulk_0 = [38.448328757254195, 7.718376151972274, 8.254653357127351, 9.95911842561036, 5.97899305676308, 0.24079752710315697, 2.2556006776515964, 0.7244006013202644, 0.7233140004182841, 0.0, 12.696417444779453];
# Define bulk-rock composition unit
sys_in = "mol"
# Choose database
data = Initialize_MAGEMin("ig", verbose=false);
# allocate storage space
Out_XY = Vector{out_struct}(undef,nsteps)
melt_F = 1.0
bulk = copy(bulk_0)
np = 0
while melt_F > 0.0
np +=1
out = single_point_minimization(P[np], T[np], data, X=bulk, Xoxides=oxides, sys_in=sys_in)
Out_XY[np] = deepcopy(out)
# retrieve melt composition to use as starting composition for next iteration
melt_F = out.frac_M
bulk .= out.bulk_M
print("#$np P: $(round(P[np],digits=3)), T: $(round(T[np],digits=3))\n")
print(" ---------------------\n")
print(" melt_F: $(round(melt_F, digits=3))\n melt_composition: $(round.(bulk ,digits=3))\n\n")
end
ndata = np -1 # last point has melt fraction = 0
x = Vector{String}(undef,ndata)
melt_SiO2_anhydrous = Vector{Float64}(undef,ndata)
melt_FeO_anhydrous = Vector{Float64}(undef,ndata)
melt_H2O = Vector{Float64}(undef,ndata)
fluid_frac = Vector{Float64}(undef,ndata)
melt_density = Vector{Float64}(undef,ndata)
residual_density = Vector{Float64}(undef,ndata)
system_density = Vector{Float64}(undef,ndata)
for i=1:ndata
x[i] = "[$(round(P[i],digits=3)), $(round(T[i],digits=3))]"
melt_SiO2_anhydrous[i] = Out_XY[i].bulk_M[1] / (sum(Out_XY[i].bulk_M[1:end-1])) * 100.0
melt_FeO_anhydrous[i] = Out_XY[i].bulk_M[5] / (sum(Out_XY[i].bulk_M[1:end-1])) * 100.0
melt_H2O[i] = Out_XY[i].bulk_M[end] *100
fluid_frac[i] = Out_XY[i].frac_F*100
melt_density[i] = Out_XY[i].rho_M
residual_density[i] = Out_XY[i].rho_S
system_density[i] = Out_XY[i].rho
end
# section to plot composition evolution
trace1 = scatter( x = x,
y = melt_SiO2_anhydrous,
name = "Anyhdrous SiO₂ [mol%]",
line = attr( color = "firebrick",
width = 2) )
trace2 = scatter( x = x,
y = melt_FeO_anhydrous,
name = "Anyhdrous FeO [mol%]",
line = attr( color = "royalblue",
width = 2) )
trace3 = scatter( x = x,
y = melt_H2O,
name = "H₂O [mol%]",
line = attr( color = "cornflowerblue",
width = 2) )
trace4 = scatter( x = x,
y = fluid_frac,
name = "fluid [mol%]",
line = attr( color = "black",
width = 2) )
layout = Layout( title = "Melt composition",
xaxis_title = "PT [kbar, °C]",
yaxis_title = "Oxide [mol%]")
plot([trace1,trace2,trace3,trace4], layout)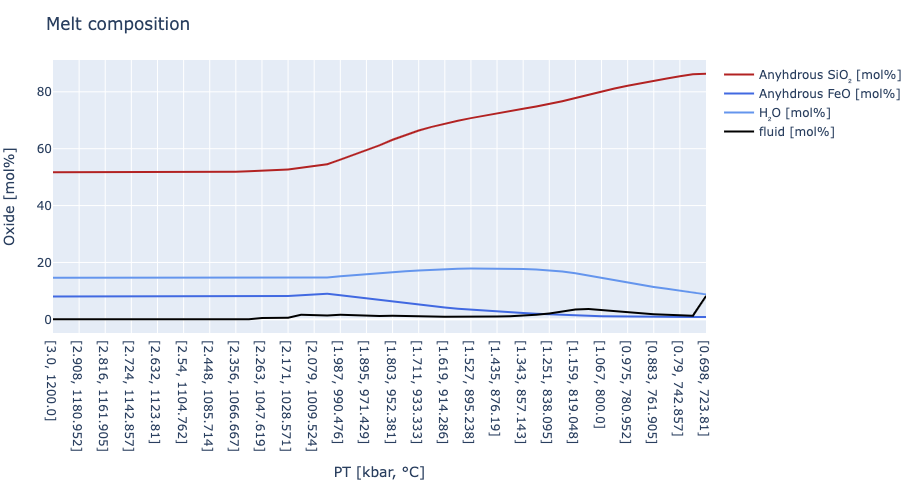
# section to plot density evolution
trace1 = scatter( x = x,
y = melt_density,
name = "Melt density [kg/m³]",
line = attr( color = "gold",
width = 2) )
trace2 = scatter( x = x,
y = residual_density,
name = "Residual density [kg/m³]",
line = attr( color = "firebrick",
width = 2) )
trace3 = scatter( x = x,
y = system_density,
name = "System density[kg/m³]",
line = attr( color = "coral",
width = 2) )
layout = Layout( title = "Density evolution",
xaxis_title = "PT [kbar, °C]",
yaxis_title = "Density [kg/³]")
plot([trace1,trace2,trace3], layout)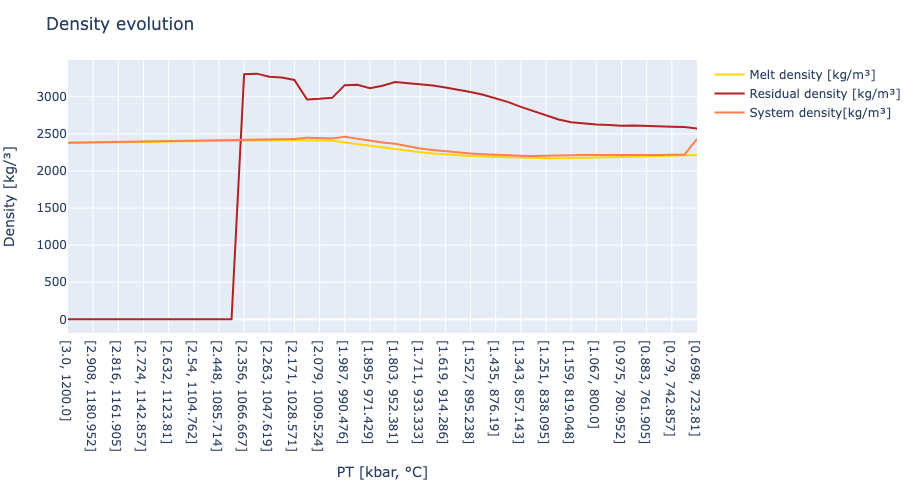
E.10 Threaded fractional crystallization
using ProgressMeter
using MAGEMin_C
using Base.Threads: @threads
function get_data_thread( MAGEMin_db :: MAGEMin_Data )
id = Threads.threadid()
gv = MAGEMin_db.gv[id]
z_b = MAGEMin_db.z_b[id]
DB = MAGEMin_db.DB[id]
splx_data = MAGEMin_db.splx_data[id]
return (gv, z_b, DB, splx_data)
end
function example_of_threaded_MAGEMin_calc( data_thread :: Tuple{Any, Any, Any, Any}, dtb :: String,
starting_P :: Float64,
starting_T :: Float64,
ending_T :: Float64,
n_steps :: Int64,
sys_in :: String,
bulk :: Vector{Float64},
Xoxides :: Vector{String} )
gv, z_b, DB, splx_data = data_thread # Unpack the MAGEMin data
Out_PT = Vector{out_struct}(undef, n_steps)
gv = define_bulk_rock(gv, bulk, Xoxides, sys_in, dtb);
for i = 1:n_steps
P = Float64(starting_P)
T = Float64(starting_T - (starting_T - ending_T) * (i-1)/(n_steps-1))
out = point_wise_minimization( P, T, gv, z_b, DB, splx_data;
name_solvus=true)
Out_PT[i] = deepcopy(out)
if "liq" in out.ph
bulk = out.bulk_M
oxides = out.oxides
gv = define_bulk_rock(gv, bulk, oxides, "mol", dtb);
end
end
return Out_PT
end
function perform_threaded_calc( Out_all :: Vector{Vector{out_struct}},
data :: MAGEMin_Data,
dtb :: String,
n_starting_points :: Int64,
starting_P :: Vector{Float64},
starting_T :: Vector{Float64},
ending_T :: Vector{Float64},
n_steps :: Int64,
sys_in :: String,
bulk :: Matrix{Float64},
Xoxides :: Vector{String} )
progr = Progress(n_starting_points, desc="Computing $n_starting_points examples of threaded MAGEMin_calc...") # progress meter
@threads :static for i=1:n_starting_points
data_thread = get_data_thread(data)
starting_P_ = starting_P[i]
starting_T_ = starting_T[i]
ending_T_ = ending_T[i]
n_steps_ = n_steps
bulk_ = bulk[i,:]
Out_PT = example_of_threaded_MAGEMin_calc( data_thread, dtb,
starting_P_,
starting_T_,
ending_T_,
n_steps_,
sys_in,
bulk_,
Xoxides )
Out_all[i] = Out_PT
next!(progr)
end
finish!(progr)
return Out_all
end
# first initialize MAGEMin
dtb = "mp"
data = Initialize_MAGEMin(dtb, verbose=-1; solver=2);
n_starting_points = 64
# Allocate memory for the output (Nested_structure where each element is a vector of gmin_struct)
Out_all = Vector{Vector{out_struct}}(undef, n_starting_points);
starting_P = [range(1.0,10.0,n_starting_points);] # 10 starting points
starting_T = ones(n_starting_points) .* 1300.0
ending_T = ones(n_starting_points) .* 600.0
n_steps = 128
sys_in = "wt"
bulk = repeat([58.509, 1.022, 14.858, 4.371, 0.141, 4.561, 5.912, 3.296, 2.399, 10.0, 0.0]', n_starting_points)
Xoxides = ["SiO2", "TiO2", "Al2O3", "FeO", "MnO", "MgO", "CaO", "Na2O", "K2O","H2O","O"]
Out_all = perform_threaded_calc(Out_all, data, dtb, n_starting_points, starting_P, starting_T, ending_T, n_steps, sys_in, bulk, Xoxides);
Finalize_MAGEMin(data)E.11 Isentropic path calculation
using MAGEMin_C
using Plots
using ProgressMeter
dtb = "ig"
data = Initialize_MAGEMin(dtb,verbose=-1);
test = 0 # KLB-1
data = use_predefined_bulk_rock(data, test);
MPT = 1350.0; # Mantle potential temperature in °C
adiabat = 0.55; # Adiabatic gradient in the upper mantle °C/km
Depth = 100.0; # Depth in km
rho_Mantle = 3300.0; # Density of the mantle in kg/m³
Ts = MPT + adiabat * Depth # Starting temperature in the isentropic path (rough estimate)
Ps = Depth*1e3*9.81*rho_Mantle/1e5/1e3 # Starting pressure in kbar (rough estimate)
Pe = 0.001; # Ending pressure in kbar
n_steps = 32; # number of steps in the isentropic path
n_max = 32; # Maximum number of iterations in the bisection method
tolerance = 0.1; # Tolerance for the bisection method
P = Array(range(Ps, stop=Pe, length=n_steps)) # Defines pressure values for the isentropic path
out = Vector{out_struct}(undef, n_steps) # Vector to store the output of the single_point_minimization function
out_tmp = out_struct;
# compute the reference entropy at pressure and temperature of reference
out[1] = deepcopy( single_point_minimization(Ps,Ts, data));
Sref = out[1].entropy # Entropy of the system at the starting point
@showprogress for j = 2:n_steps
a = out[j-1].T_C - 50.0
b = out[j-1].T_C
n = 1
conv = 0
n = 0
sign_a = -1
while n < n_max && conv == 0
c = (a+b)/2.0
out_tmp = deepcopy( single_point_minimization(P[j],c, data));
result = out_tmp.entropy - Sref
sign_c = sign(result)
if abs(b-a) < tolerance
conv = 1
else
if sign_c == sign_a
a = c
sign_a = sign_c
else
b = c
end
end
n += 1
end
out[j] = deepcopy(out_tmp)
end
Finalize_MAGEMin(data)
#=
In the following section we extract the melt fraction, total melt fraction, SiO2 in the melt, melt density for all steps
=#
S = [out[i].entropy for i in 1:n_steps]; # check entropy values
frac_M = [out[i].frac_M for i in 1:n_steps]; # Melt fraction for all steps
frac_M[frac_M .== 0.0] .= NaN; # Replace 0.0 values with NaN
T = [out[i].T_C for i in 1:n_steps]; # extract temperature for all steps
SiO2_id = findfirst(out[1].oxides .== "SiO2") # Index of SiO2 in the oxides array
dry_id = findall(out[1].oxides .!= "H2O") # Indices of all oxides except H2O
SiO2_M_dry = [ (out[i].bulk_M[SiO2_id] / sum(out[i].bulk_M[dry_id])*100.0) for i in 1:n_steps]; # SiO2 in the melt for all steps
rho_M = [ (out[i].rho_M) for i in 1:n_steps]; # melt density for all steps
rho_M[rho_M .== 0.0] .= NaN; # Replace 0.0 values with NaN
#=
Ploting the results using Plots
=#
p1 = plot(T,P, xlabel="Temperature (°C)", marker = :circle, markersize = 2, lw=2, ylabel="Pressure (kbar)", legend=false)
p2 = plot(frac_M,P, xlabel="Melt fraction (mol)", marker = :circle, markersize = 2, lw=2, ylabel="Pressure (kbar)", legend=false)
p3 = plot(rho_M,P, xlabel="Melt density (kg/m³)", marker = :circle, markersize = 2, lw=2, ylabel="Pressure (kbar)", legend=false)
p4 = plot(SiO2_M_dry,P, xlabel="SiO₂ melt anhydrous (mol%)", marker = :circle, markersize = 2, lw=2, ylabel="Pressure (kbar)", legend=false)
fig = plot(p1, p2, p3, p4, layout=(2, 2), size=(800, 600))
savefig(fig,"isentropic_path.png")References
Green, ECR, Holland, TJB, Powell, R, Weller, OM, & Riel, N (2025). Journal of Petrology, 66, doi: 10.1093/petrology/egae079
Weller, OM, Holland, TJB, Soderman, CR, Green, ECR, Powell, R, Beard, CD & Riel, N (2024). New Thermodynamic Models for Anhydrous Alkaline-Silicate Magmatic Systems. Journal of Petrology, 65, doi: 10.1093/petrology/egae098
Holland, TJB, Green, ECR & Powell, R (2022). A thermodynamic modelfor feldspars in KAlSi3O8-NaAlSi3O8-CaAl2Si2O8 for mineral equilibrium calculations. Journal of Metamorphic Geology, 40, 587-600, doi: 10.1111/jmg.12639
Tomlinson, EL & Holland, TJB (2021). A Thermodynamic Model for the Subsolidus Evolution and Melting of Peridotite. Journal of Petrology,62, doi: 10.1093/petrology/egab012
Holland, TJB, Green, ECR & Powell, R (2018). Melting of Peridotitesthrough to Granites: A Simple Thermodynamic Model in the System KNCFMASHTOCr. Journal of Petrology, 59, 881-900, doi: 10.1093/petrology/egy048
Green, ECR, White, RW, Diener, JFA, Powell, R, Holland, TJB & Palin, RM (2016). Activity-composition relations for the calculationof partial melting equilibria in metabasic rocks. Journal of Metamorphic Geology, 34, 845-869, doi: 10.1111/jmg12211
White, RW, Powell, R, Holland, TJB, Johnson, TE & Green, ECR (2014). New mineral activity-composition relations for thermodynamic calculations in metapelitic systems. Journal of Metamorphic Geology, 32, 261-286, doi: 10.1111/jmg.12071
Holland, TJB & Powell, RW (2011). An improved and extended internally consistent thermodynamic dataset for phases of petrological interest, involving a new equation of state for solids. Journal of Metamorphic Geology, 29, 333-383, doi: 10.1111/j.1525-1314.2010.00923.x